Reflector
Y la parábola tiene la siguiente propiedad sorprendente:
Un rayo paralelo al eje de simetría se refleja en la superficie directamente hacia el foco.
Así las parábolas se pueden usar para:
| 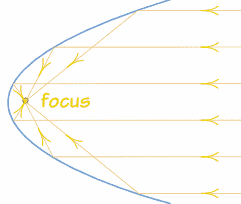 |
| Y por eso el punto central se llama foco... ¡porque ahí es donde se enfocan todos los rayos! |  |
 |
También sale una parábola cuando seccionas un cono (el corte tiene que ser paralelo al lado del cono).
Por tanto, la parábola es una sección cónica (una sección de un cono).
|
Ecuaciones
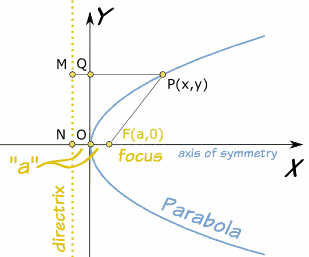
Si pones la parábola en coordenadas cartesianas (gráfico x-y) con:
entonces la curva queda definida por la ecuación:
y2 = 4ax
|  |
Ejemplo: ¿dónde está el foco de la ecuación y2=5x ?
Si ponemos y2 = 5x en la forma y2 = 4ax, tenemos que y2 = 4 (5/4) x,
así que a = 5/4, y el foco de y2=5x es:
F = (a,0) = (5/4,0)
Las ecuaciones de las parábolas en las distintas orientaciones son:
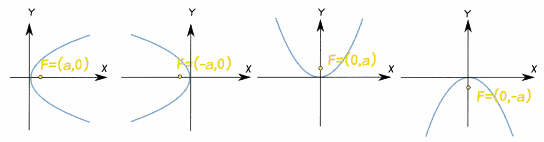 | |||
| y2 = 4ax | y2 = -4ax | x2 = 4ay | x2 = -4ay |
Medidas para una antena parabólica
Si quieres construir una antena parabólica que tenga el foco 200 mm sobre la superficie, ¿qué medidas necesitas?
Para que sea fácil de hacer, digamos que apunte hacia arriba, y así tenemos la ecuación x2 = 4ay.
Y queremos que "a" sea 200, así que la ecuación queda:
x2 = 4ay = 4 × 200 × y = 800y
Lo reescribimos para poder calcular las alturas:
y = x2/800
Aquí tienes algunas medidas de alturas que van saliendo:
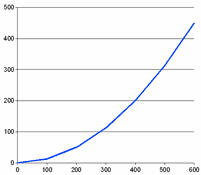 | Distancia horizontal ("x") | Altura ("y") |
| 0 mm | 0.0 mm | |
| 100 mm | 12.5 mm | |
| 200 mm | 50.0 mm | |
| 300 mm | 112.5 mm | |
| 400 mm | 200.0 mm | |
| 500 mm | 312.5 mm | |
| 600 mm | 450.0 mm | |