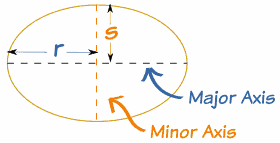
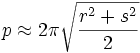Parábolas y Elipse: junio 2016

Ecuación reducida de la elipse

Tomamos como centro de la elipse el centro de coordenadas y los ejes de la elipse como ejes de coordenadas. Las coordenadas de los focos son:

F'(-c,0) y F(c,0)

Cualquier punto de la elipse cumple:

Esta expresión da lugar a:

Realizando las operaciones llegamos a:

Ejemplo

Hallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3,0) y F(3, 0), y su eje mayor mide 10.

Semieje mayor

Semidistancia focal

Semieje menor

Ecuación reducida

Excentricidad

Ecuación reducida de eje vertical de la elipse

Si el eje principal está en el de ordenadas se obtendrá la siguiente ecuación:

Las coordenadas de los focos son:

F'(0, -c) y F(o, c)

Ejemplo

Dada la ecuación reducida de la elipse

, hallar las coordenadas de los vértices de los focos y la excentricidad.

Ecuación de la elipse

Si el centro de la elipse C(x₀,y₀) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X₀+c, y₀) y F'(X₀-c, y₀). Y la ecuación de la elipse será:

Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:

Donde A y B tienen el mismo signo.

Ejemplos

Hallar la ecuación de la elipse de foco F(7, 2), de vértice A(9, 2) y de centro C(4, 2).

Dada la elipse de ecuación

, hallar su centro, semiejes, vértices y focos.

Ecuación de eje vertical de la elipse

Si el centro de la elipse C(x₀,y₀) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(X₀, y+c) y F'(X₀, y₀-c). Y la ecuación de la elipse será:

Elementos de la elipse.

Focos: Son los puntos fijos F y F'.
Eje focal: Es la recta que pasa por los focos.
Eje secundario: Es la mediatriz del segmento FF'.
Centro: Es el punto de intersección de los ejes.
Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.

Distancia focal: Es el segmento de longitud 2c, c es el valor de la semidistancia focal.
Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
Eje mayor: Es el segmento de longitud 2a, a es el valor del semieje mayor.
Eje menor:Es el segmento de longitud 2b, b es el valor del semieje menor.
Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.

Relación entre la distancia focal y los semiejes

Calculando

Área

El área de una elipse es π × r × s

(Si es una circunferencia, r y s son iguales, y sale π × r × r = πr², ¡que es correcto!)

Aproximación al perímetro

Aunque parezca extraño, el perímetro de una elipse es muy difícil de calcular, así que he creado una página especial para ese tema: lee Perímetro de una elipse para ver los detalles.

Pero una aproximación sencilla que está a menos de 5% del valor correcto (siempre que r no sea más de 3 veces s) es la siguiente:

Obtención de los ejes reales, a partir de dos ejes conjugados de una elipse.

Dados los ejes conjugados de una elipse A’B’ y C’D’, podremos obtener a partir de ellos los ejes reales de la elipse, para ello seguiremos los siguientes pasos:

1.- Por O, centro de la elipse, trazaremos la perpendicular al eje conjugado A’B’, y sobre el llevaremos la distancia O-A’, determinando el punto 1.
2.- Uniremos el punto 1 con C’, y determinaremos el punto medio 2, de dicho segmento.
3.- Con centro en 2, trazaremos un arco de radio 2-O, que determinará sobre la prolongación del segmento 1-C’, los puntos 3 y 4. Las rectas O-3 y O-4 determinan las direcciones perpendiculares de los ejes reales de la elipse.
4.- Con centro en 2 trazaremos la circunferencia de diámetro 1-C’. Uniendo el centro O con 2, determinaremos sobre dicha circunferencia, los puntos 5 y 6, siendo las distancias O-5 y O-6, las dimensiones de los semiejes reales de la elipse.
5.- Solo resta llevar, mediante los correspondientes arcos de circunferencias, las dimensiones anteriores sobre las direcciones de los ejes, obteniendo así los ejes reales de la elipse AB y CD.

Trazado de la elipse mediante radios vectores

Teniendo en cuenta la definición de la elipse, como el lugar geométrico de los puntos del plano, cuya suma de distancias a los focos es igual a 2a, longitud del eje mayor de la elipse, solo necesitaremos coger pares de radios vectores, cuya suma sea 2a, para ello determinaremos una serie de puntos sobre el eje mayor 1, 2, 3etc., y cogeremos como parejas de radios vectores, los segmentos A1-B1, A2-B2, A3-B3, y así sucesivamente, determinando los puntos 1′, 2′, 3′, etc. de la elipse.

Con cada pareja de radios vectores, se determinarán cuatro puntos de la elipse, uno en cada cuadrante de la misma.

Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la elipse, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.

Trazado de la elipse por haces proyectivos

Trazaremos el rectángulo AOCE, y dividiremos los lados AO y AE en un mismo número de partes iguales.

Seguidamente iremos trazando las rectas C1-D1, C2-D2, etc. y en sus intersecciones iremos obteniendo puntos de la elipse. Esto se repetirá para los cuatro cuadrantes de la elipse.

Elipse

La elipse es una curva cerrada y plana, que se define como el lugar geométrico de los puntos del plano cuya suma de distancias r+r’, a dos puntos fijos F y F’, denominados focos, es constante e igual a 2a, siendo 2a la longitud del eje mayor A-B de la elipse.

La elipse tiene dos eje, el eje mayor A-B, también llamado real, y el eje menor C-D, ambos se cruzan perpendicularmente en el centro O de la elipse.

La longitud del eje mayor es 2a, la del eje menor 2b y la distancia focal 2c, y se cumple que a² = b² + c².

La elipse es simétrica respecto a los dos ejes.

Las rectas que unen un punto cualquiera de la elipse P, con los focos, se denominan radios vectores r y r’, y por definición se cumple que r + r’ = 2a.

Propiedades y elementos

Se denomina circunferencia principal Cp, a la circunferencia de centro O, y diámetro 2a. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la elipse. También se puede definir como el punto medio de los segmentos que unen un foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la elipse

Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la elipse, y radio 2a. En una elipse se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la elipse.

Observando la figura, también podemos definir la elipse, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.

Concepto de diámetros conjugados

Si tenemos un diámetro de la elipse A’B’, el diámetro conjugado con él, es el lugar geométrico de los centros de las cuerdas paralelas a dicho diámetro (1, 2, 3, 4, etc.), estos centros determinan el diámetro conjugado D’C’ del dado.

Los ejes reales de la elipse, son los únicos diámetros conjugados perpendiculares entre si.

Mediante dos diámetros conjugados, podremos construir la elipse directamente, o bien obtener los ejes reales de la misma.

Ejercicios resueltos.

Determinar, en forma reducida, las ecuaciones de las siguientes parábolas, indicando el valor del parámetro, las coordenadas del foco y la ecuación de la directriz.